32. Quiz: Optimal Policies
Quiz: Optimal Policies
If the state space \mathcal{S} and action space \mathcal{A} are finite, we can represent the optimal action-value function q_* in a table, where we have one entry for each possible environment state s \in \mathcal{S} and action a\in\mathcal{A}.
The value for a particular state-action pair s,a is the expected return if the agent starts in state s, takes action a, and then henceforth follows the optimal policy \pi_*.
We have populated some values for a hypothetical Markov decision process (MDP) (where \mathcal{S}={ s_1, s_2, s_3 } and \mathcal{A}={a_1, a_2, a_3}) below.

You learned in the previous concept that once the agent has determined the optimal action-value function q_, it can quickly obtain an optimal policy \pi_ by setting \pi_(s) = \arg\max_{a\in\mathcal{A}(s)} q_(s,a) for all s\in\mathcal{S}.
To see why this should be the case, note that it must hold that v_(s) = \max_{a\in\mathcal{A}(s)} q_(s,a).
In the event that there is some state s\in\mathcal{S} for which multiple actions a\in\mathcal{A}(s) maximize the optimal action-value function, you can construct an optimal policy by placing any amount of probability on any of the (maximizing) actions. You need only ensure that the actions that do not maximize the action-value function (for a particular state) are given 0% probability under the policy.
Towards constructing the optimal policy, we can begin by selecting the entries that maximize the action-value function, for each row (or state).
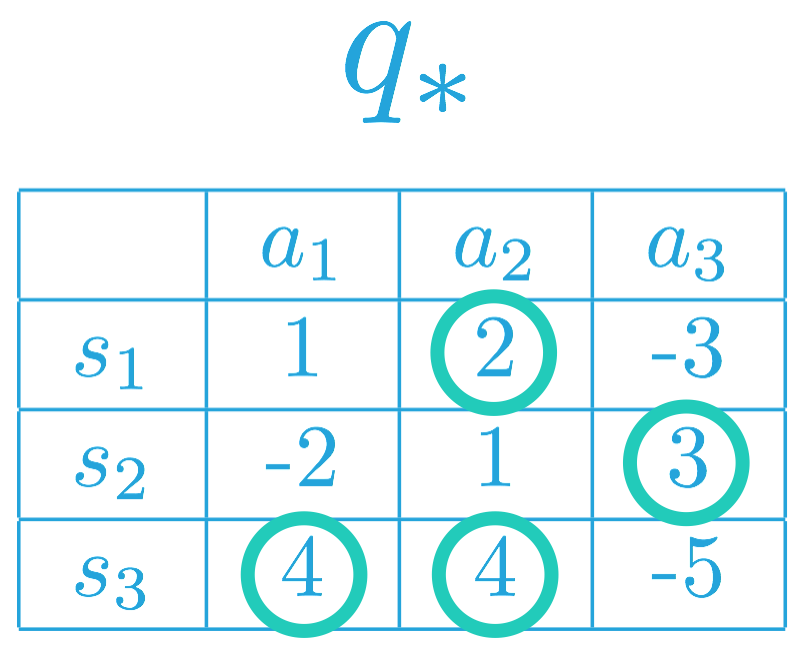
Thus, the optimal policy \pi_* for the corresponding MDP must satisfy:
- \pi_(s_1) = a_2 (or, equivalently, \pi_(a_2| s_1) = 1), and
- \pi_(s_2) = a_3 (or, equivalently, \pi_(a_3| s_2) = 1).
This is because a_2 = \arg\max_{a\in\mathcal{A}(s_1)}q_(s_1,a), and a_3 = \arg\max_{a\in\mathcal{A}(s_2)}q_(s_2,a).
In other words, under the optimal policy, the agent must choose action a_2 when in state s_1, and it will choose action a_3 when in state s_2.
As for state s_3, note that a_1, a_2 \in \arg\max_{a\in\mathcal{A}(s_3)}q_(s_3,a). Thus, the agent can choose either action a_1 or a_2 under the optimal policy, but it can never choose action a_3. That is, the optimal policy \pi_ must satisfy:
- \pi_*(a_1| s_3) = p,
- \pi_*(a_2| s_3) = q, and
- \pi_*(a_3| s_3) = 0,
where p,q\geq 0, and p + q = 1.
Question
Consider a different MDP, with a different corresponding optimal action-value function. Please use this action-value function to answer the following question.
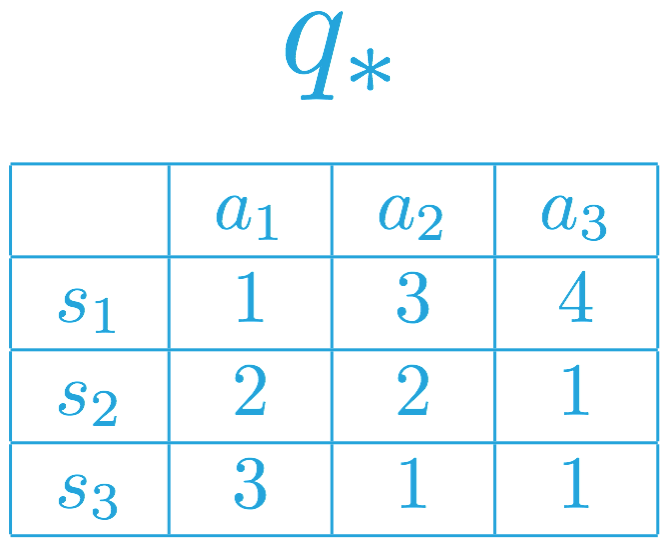
SOLUTION:
- The agent always selects action a_3 in state s_1.
- The agent is free to select either action a_1 or action a_2 in state s_2.
- The agent must select action a_1 in state s_3.